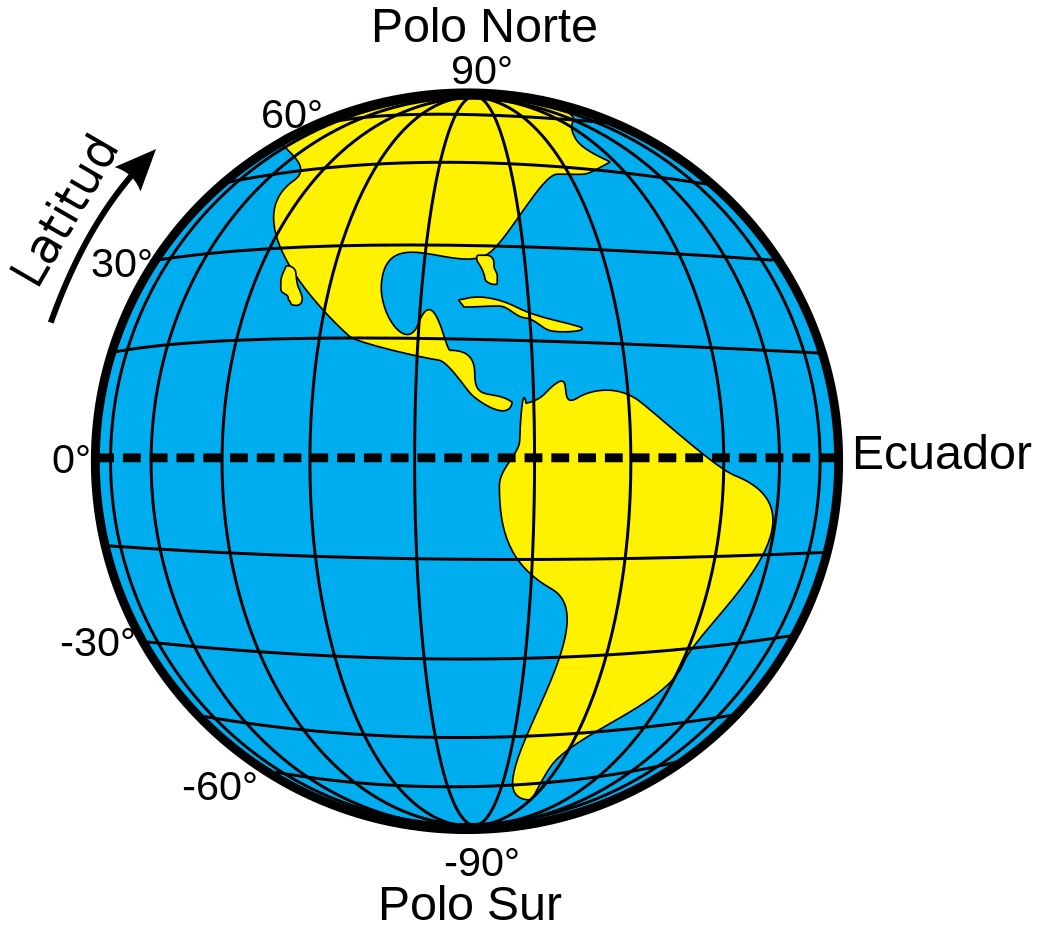
Calculando la latitud a la que se encuentra Artaj (1). Punto Aries. El equinoccio de primavera.

Ya llega la primavera, y no es por que lo diga El Corte Inglés :-). Hoy es 20 de Marzo de 2024 y el equinoccio de primavera (en el hemisferio norte, en el sur es el equinoccio de otoño) ha ocurrido a las 3:06 UTC (4:06 en España).  Equinoccio significa "igualdad entre el día y la noche". Cada año, hay dos días en los que cada lugar de la Tierra recibe aproximadamente la misma cantidad de luz solar (12 horas): son los equinoccios. Es decir, dura lo mismo el dia que la noche.

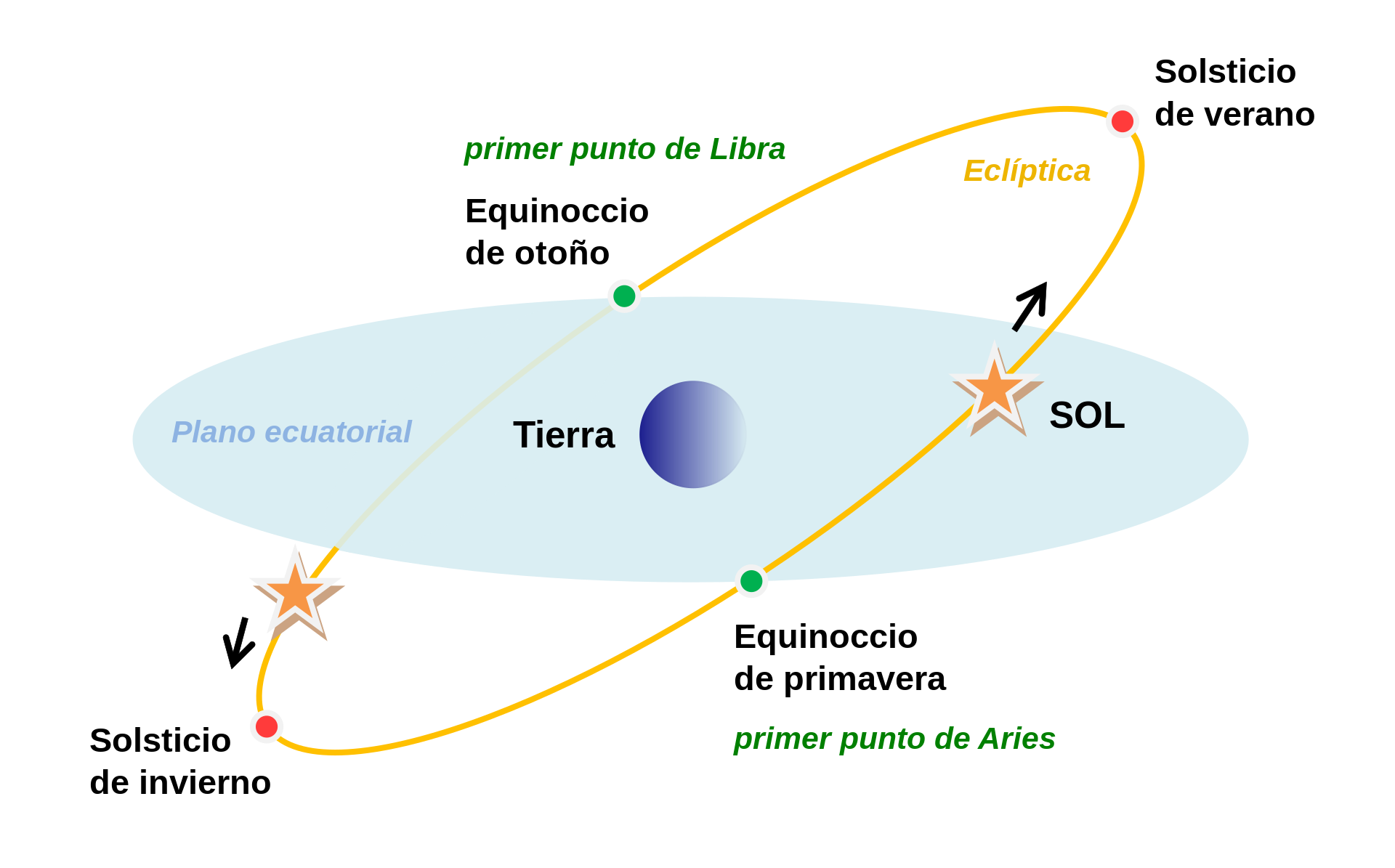
Como bien sabemos, la tierra orbita alrededor del sol. A la trayectoria por donde "aparentemente" (es decir, visto desde la Tierra) transcurre el sol se le llama eclíptica. La oblicuidad de la eclíptica es el término utilizado por los astrónomos para designar la inclinación del ecuador de la Tierra con respecto a la eclíptica, o del eje de rotación de la Tierra con respecto a una perpendicular a la eclíptica. Actualmente es de 23° 26′ 11″

La oblicuidad de la eclíptica fue medida por el griego Eratóstenes en el siglo III a. C.

El plano de la eclíptica se interseca con el plano del ecuador celeste en dos puntos opuestos denominados equinoccios (ver imagen de portada). Justo en esos dos dias, el eje de rotación de la tierra forma un ángulo de 90º con la línea imaginaria que une la tierra y el sol y en consecuencia el ángulo que el sol forma con un lugar cualquiera de la tierra determina exactamente la latitud de ese lugar.

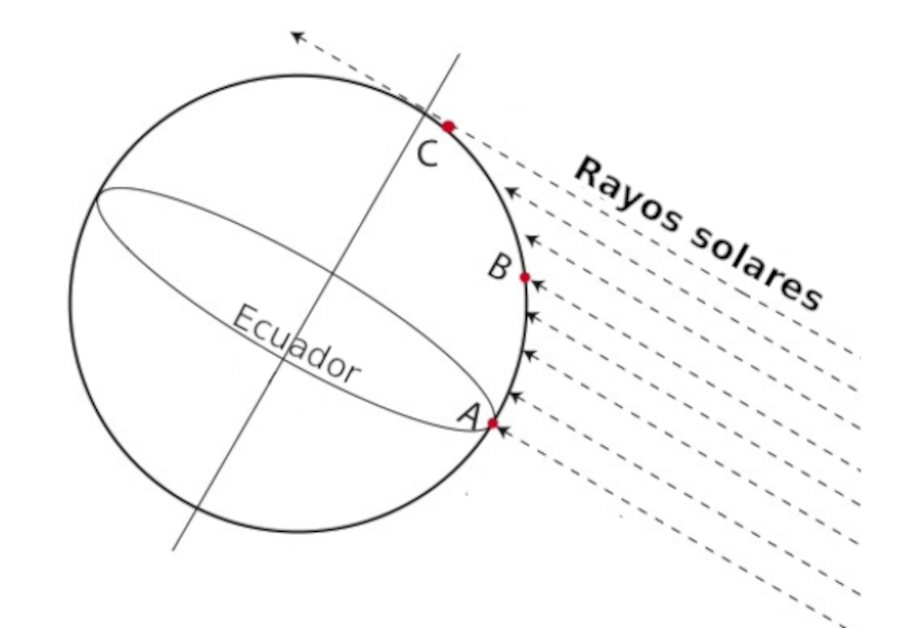
Si nos fijamos en el gráfico y debido a que vivimos en una esfera, vemos que solo en el en el ecuador, al alcanzar su cenit el sol (al mediodía), los rayos del sol llegarán perpendiculares por lo que ningún objeto proyectará sombra alguna.

Si nos vamos alejando del ecuador, la inclinación con el que llegan los rayos solares va aumentando y producirán sombras sobre los objetos. Esta medida de la sombra es la que nos va a decir a que latitud nos encontramos.

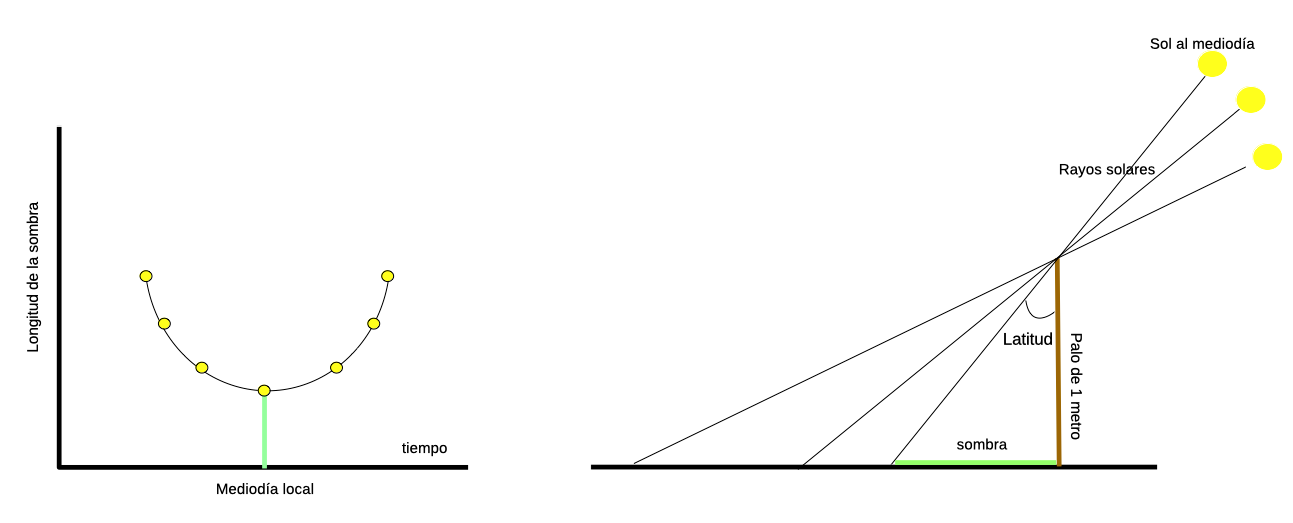
Tenemos que buscar un lugar que sea llano y nivelado, porque sino las mediciones no van a salir bien.

• Clavamos un palo completamente vertical
• Medimos exactamente la longitud del palo desde la base (tierra) hasta el extremo superior.
• Vamos haciendo mediciones cada cierto tiempo de la longitud de la sombra que va proyectando.
• La sombra mas corta corresponde al momento en el que el sol está en su máxima altura, es decir, es el mediodía local.

Calcular la latitud ahora, sabiendo la longitúd del palo y la longitud de la sombra es muy sencillo. Es trigonometría básica.

La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto al ángulo y el cateto adyacente.

tg (latitud) = longitud sombra mínima / longitud del palo

Por lo que  calculando la inversa de la tangente calculamos el ángulo, es decir, la latitud

latitud = Arctg (tg (latitud))

Hoy no ha sido un buen día en Artaj para medir la sombra, ya que el cielo está cubierto al 100%, pero próximamente haré un video con todo el proceso. Mientras tanto quedemonos en que Google maps nos indica que la latitud de artaj es 39°48'08.8"N

BONUS:

Eratóstenes de Cirene (276 a.C.- 194 a.C) fué un matemático, astrónomo y geógrafo, conocido por ser la primera persona que calculó el diámetro y la circunferencia de la Tierra, además de calcular la inclinación del eje de la Tierra. Ambas mediciones fueron notablemente precisas para el tiempo en el que vivió, así como los instrumentos con los que contaba.

Eratóstenes sabía que en Siena (Actualmente Assuán, en Egipto, situada muy aproximadamente en el trópico de Cáncer) el día del solsticio de verano (21 de Junio) los objetos verticales no producían ninguna sombra. Al estar tan alejado el Sol de la Tierra podía dar por válido que los rayos solares eran paralelos, por lo que midió la sombra que se producía en Alejandría (que aproximadamente se encuentra en el mismo meridiano) el día del solsticio de verano al mediodía (lo mismo que hemos hecho aquí, pero en el equinoccio de primavera, para calcular la latitud de Artaj). Con ello calculó que el cenit de Siena distaba 7º 12' del de Alejandría ( 1/50 parte de la circunferencia terrestre). La distancia estimada entre ambas ciudades la fijó en 5000 "estadios", por lo que dedujo que la circunferencia de la tierra era de 252.000 "estadios" aproximadamente. Asumiendo que el "estadio" que utilizaba Eratóstenes era el equivalente a 184,8 metros da como resultado longitud de la circunferencia de 46.200 km, cuando en realidad es 40.075 km. Es decir, un error del 15 %. SI asumimos que utilizó el estadio egipcio, apróx. 158 metros, el calculo de la circunferencia es de 39.614 km,es decir, que no llega a un 2% de error.

Aunque hay que considerar que existen diversos errores en las suposiciones que hizo (Alejandría y Siena estan separadas 843 km y no los 924 que calculó Eratóstenes, o que ambas ciudades no estan en el mismo meridiano, estan separadas 3 grados, etc..) lo que si es cierto es la validez del método utilizado para calcular la circunferencia de la Tierra. Y eso fue hace más de 2.200 años.